动态规划之01背包
(广东工业大学 2022 寒假集训 专题二)
洛谷P1048采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 2 个整数 T(1≤T≤1000)和 M(1≤M≤100),用一个空格隔开,T 代表总共能够用来采药的时间,M 代表山洞里的草药的数目。
接下来的 M 行每行包括两个在 1 到 100 之间(包括 1 和 100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入输出样例

说明/提示
【数据范围】
对于 30% 的数据,M≤10;
对于全部的数据,M≤100。
【题目来源】
NOIP 2005 普及组第三题
讲解:
01背包问题的特点是选与不选,每个物品只有一个,选了就没有了。
既然是动态规划,那么我们就有dp数组,这里我们构建二维数组能方便理解01背包(没有为什么,就是二维数组),dp[i][j]表示我们选i件物品和有j背包容量时,能挣的最多的钱;我们假设有四个物品(物品重量 和 取得这个物品能挣多少钱)和10g的背包容量。表格中横向是背包容量(从0到10),纵向是选择的物品数量(0到4,用数组存物品重量m[1~4])。那么我们就是要求dp[4][10]。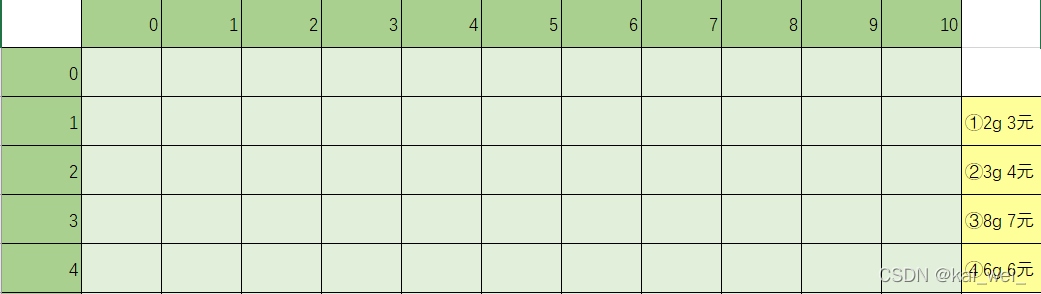
1、为什么要有横轴表示背包的容量从0到10?
可以看一个例子,假如我们装物品装到第四件(6g 6元),我们的选择是带走它,那么此时背包就只剩10-6=4g,如果我们求了背包容量为4时的最大值(挣的钱的最大值),我们只要两者加起来就能得到这种情况下(带走第四件物品)的结果。
2、为什么要纵轴表示选取物品从0件到4件?
可以按照正常人思维想,拿物品不就是一个一个拿的吗?(bushi),其实这样我们可以求得拿1件物品/拿两件物品…所挣的最大钱数。
第一行:0个物品当然挣0元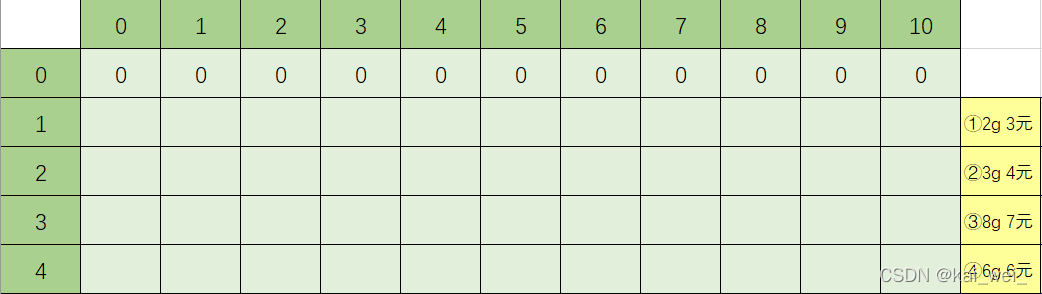
第二行: 我们拿第一件物品,2g 3元,背包容量为0时,放不下,因此我们不选;为1时,也放不下,但是2~10都能放得下,所以后面我们选,都能挣钱,(dp[1][10]代表拿一件物品时10背包容量所挣的最多的钱,确实是3)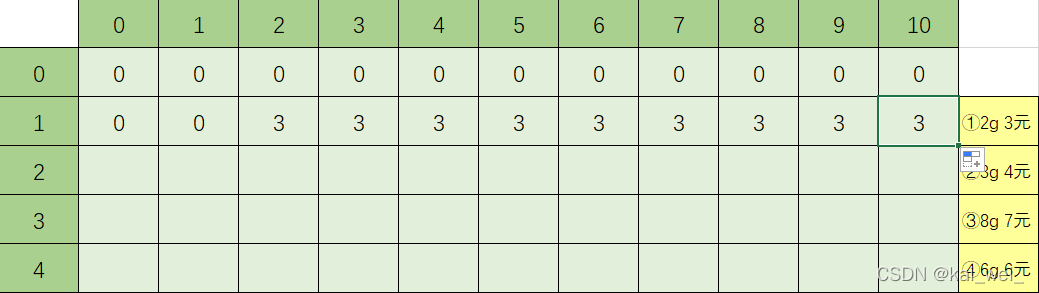
第三行: 我们拿第二件物品,3g4元,同样,0 1 2个背包容量装不下,因此我们不选,那么就和前一行一样,相当于我们选第1个物品,而不选第二个。当容量为3时我们1有两种选择,选和不选,1、如果选,那么此时背包用了3个容量只剩下0的容量,我们已经选了这个物品,所以我们要在前一行找,也就是dp[2][3]=dp[1][0]=0,dp[1][0]+m[2]=0+4=4,2、如果不选,那么就是选一个物品,是前一行的dp[1][3]=3,很明显4大于3,我们选4。以此类推… 把剩下的解决后得到表格,答案就是dp[4][10]=10
把剩下的解决后得到表格,答案就是dp[4][10]=10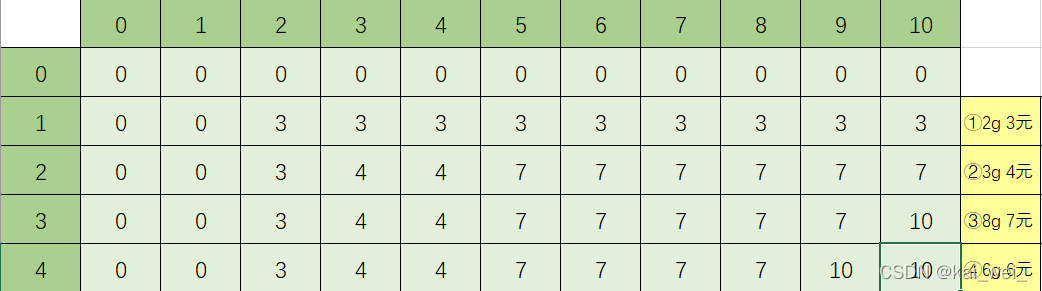
总结:这里的转移方程为dp[ i ] [ j ]=max(dp[ i-1 ] [ j ],dp[ i -1] [ j - m [ i ] ]+val[i])
二维数组只是方便理解,我我们发现dp[ i ] [ j ]只会和前一行有关,所以我们可以用一维滚动数组来实现。dp[j]=max(dp[j],dp[j-m[i]]+val[i]);
在b站找嘉特的动态规划视频有详细解释,我就是在那学的,这里懒得再打了。模板参考ac代码:
1 |
|

