CF 300C - Beautiful Numbers 数论

发表于 | | 阅读量 | 次阅读

(广东工业大学 ACM寒假集训 专题四 C）
题目链接：CF 300C - Beautiful Numbers
洛谷链接：CF 300C - Beautiful Numbers
更好的阅读体验请到这里

题目描述（洛谷翻译）：
题意翻译
Vitaly有一些奇怪的癖好，比如他特别爱两个小于10的数字a和b。Vitaly定义十进制表示下每一位都是a或b的数为“好数”，一个每一位数加起来为“好数”的“好数”被称为“极好的数”。

举个栗子=w=，如果偏爱数字为1和3，那么1212不是“好数”，13和311是“好数”，111是“极好的数”。

现在Vitaly想知道，长度为n（长度不包括前导0）的“极好的数”有多少个。对1e9+7取模。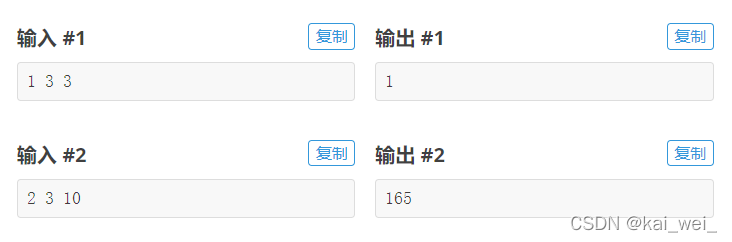
在这里插入图片描述

读题

1、有两个数字a，b。
2、“好数”是只由a,b构成的长度为n的数。
3、”好数”中每一位之和也是”好数”的数，叫“极好的数”。
4、题目要我们找“极好的数”（以下简称极好数）。
5、答案取模1e9+7，为质数。

总体思路：
因为我们找的极好数来自好数，那么我们只要枚举长度为n的所有好数，判断是不是每一位之和为好数，是的话说明是极好数，结果累加起来就可以了。
如何枚举：
一个一个数枚举是不可能的，有1000000位数呢….但是仔细想一下，数的长度是固定为n的，且只有a,b，那么我们是不是就可以枚举a的数量i，那么b的数量一定是n-i，这时候这么多个a和b组成的数就相当于i个a去放n个空位(组合数),所以就是C（n,i）（n在下，i在上）。
如何求这个组合数：
简单，运用组合数公式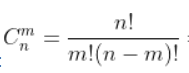：在这里插入图片描述
答案怎么求，如何求mod：
我们不是求出来之后才取模。

分析：
每个答案是一个组合数，但是组合数是一个分式，因为太大了，我们不能求出阶乘后再除下面的阶乘，我们要除数取模。
（a/b）mod p ≠(a mod p/ b mod p)mod p
这里我们要用费马小定理求逆元：
$$
\frac{n!}{i!(n-i)!}
$$
由公式可知，我们要求 i! 和(n-i)!的逆元，让他变成乘法来取模。因为p是质数，所以可以用费马小定理，用快速幂求逆元。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>//组合数，费马小定理，快速幂,逆元
using namespace std;
const long long mod=1e9+7;
long long fact[1000005];
long long a,b,n,ans=0;
bool good(long long x){
    while(x){
        long long tmp=x%10;
        if(tmp!=a && tmp!=b)return false;
        x/=10;
    }
    return true;
}
long long fastpow(long long f,long long p){
    if(p==0)return 1;
    long long res=1;
    while(p){
        if(p&1)res=res*f%mod;
        f=f*f%mod;//反正每次模就行，不要让他超longlong
        p>>=1;
    }
    return res;
}
int main()
{
    cin>>a>>b>>n;
    fact[0]=1;
    for(int i=1;i<=n;i++)fact[i]=fact[i-1]*i%mod;//打表，每次取模
    for(int i=0;i<=n;i++){
        if(good(a*i+b*(n-i))){
            long long tmp1=fastpow(fact[i],mod-2)%mod;//费马小定理求逆元
            long long tmp2=fastpow(fact[n-i],mod-2)%mod;//求完就取模
            ans+=fact[n]*tmp1%mod*tmp2%mod;//因为n!已经取过模了，所以是后面两个取
        }
    }
    printf("%lld\n",ans%mod);//这里模不模都可以
}

好像也讲的不清楚….

赞助一下作者啦
0%